חוק אוהם לשרשרת שלמה ולקטע של שרשרת: אפשרויות לכתיבת הנוסחה, תיאור והסבר
אין שום דרך לחשמלאי מקצועי או מומחה אלקטרוניקה לעקוף את חוק אוהם בפעילותו שלו, ולפתור בעיות הקשורות להגדרה, התאמה ותיקון של מעגלים אלקטרוניים וחשמליים.
למעשה, כולם צריכים להבין את החוק הזה. כי כל אחד צריך להתמודד עם חשמל בחיי היומיום.
ולמרות שחוק הפיזיקאי הגרמני אוהם נקבע בתכנית הלימודים בבית הספר העל-יסודי, בפועל הוא לא תמיד נלמד בזמן. לכן, בחומר שלנו נשקול נושא כל כך רלוונטי לחיים ונבין את האפשרויות לכתיבת הנוסחה.
תוכן המאמר:
מקטע בודד ומעגל חשמלי שלם
בהתחשב במעגל חשמלי מנקודת המבט של החלת חוק אוהם על מעגל, יש לשים לב לשתי אפשרויות חישוב אפשריות: עבור סעיף נפרד ועבור מעגל מלא.
חישוב הזרם של קטע מעגל חשמלי
קטע של מעגל חשמלי, ככלל, נחשב לחלק של המעגל שאינו כולל את מקור EMF, כבעל התנגדות פנימית נוספת.
לכן, נוסחת החישוב, במקרה זה, נראית פשוטה:
I = U/R,
איפה, בהתאמה:
- אני - חוזק הנוכחי;
- U - מתח מופעל;
- ר - התנגדות.
הפרשנות של הנוסחה פשוטה - הזרם הזורם בקטע מסוים של המעגל הוא פרופורציונלי למתח המופעל עליו, וההתנגדות פרופורציונלית הפוך.
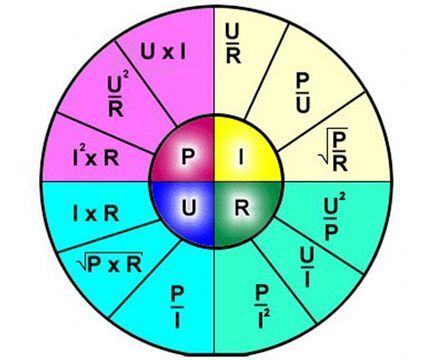
לפיכך, הנוסחה מתארת בבירור את התלות של זרימת הזרם דרך קטע נפרד של המעגל החשמלי ביחס לערכים מסוימים של מתח והתנגדות.
הנוסחה נוחה לשימוש, למשל, בעת חישוב הפרמטרים של ההתנגדות שיש להלחים במעגל אם המתח והזרם ניתנים.
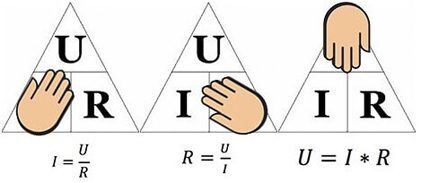
האיור שלעיל יעזור לקבוע, למשל, את הזרם הזורם דרך התנגדות של 10 אוהם עליה מופעל מתח של 12 וולט. בהחלפת הערכים, אנו מוצאים - I = 12 / 10 = 1.2 אמפר.
הבעיות של מציאת התנגדות (כאשר הזרם והמתח ידועים) או המתח (כאשר המתח והזרם ידועים) נפתרות בצורה דומה.
לפיכך, אתה תמיד יכול לבחור את מתח ההפעלה הנדרש, את עוצמת הזרם הנדרשת ואת אלמנט ההתנגדות האופטימלי.
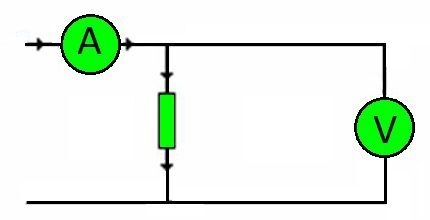
אגב, החוטים המחברים של כל מעגל הם התנגדויות. כמות העומס שהם צריכים לשאת נקבעת על ידי המתח.
בהתאם, שוב באמצעות חוק אוהם, ניתן לבחור במדויק את חתך המוליך הנדרש, בהתאם לחומר הליבה.
יש לנו הנחיות מפורטות באתר שלנו חישוב חתך כבל מבחינת כוח וזרם.
אפשרות חישוב לשרשרת שלמה
מעגל שלם מורכב מקטע (חתכים), כמו גם מקור של EMF. כלומר, למעשה, ההתנגדות הפנימית של מקור EMF מתווספת לרכיב ההתנגדות הקיים של קטע המעגל.
לכן, הגיוני לשנות מעט את הנוסחה לעיל:
I = U / (R + r)
כמובן, הערך של ההתנגדות הפנימית של EMF בחוק אוהם עבור מעגל חשמלי שלם יכול להיחשב זניח, אם כי ערך התנגדות זה תלוי במידה רבה במבנה של מקור EMF.
עם זאת, בעת חישוב מעגלים אלקטרוניים מורכבים, מעגלים חשמליים עם מוליכים רבים, נוכחות של התנגדות נוספת היא גורם חשוב.
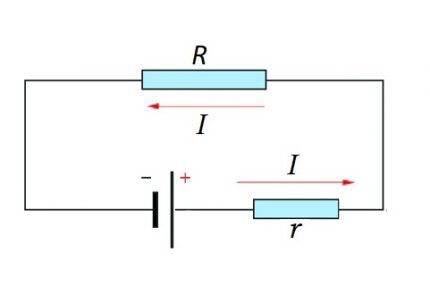
הן עבור קטע של מעגל והן עבור מעגל שלם, יש לקחת בחשבון את המומנט הטבעי - שימוש בזרם קבוע או משתנה.
אם הנקודות שצוינו לעיל, האופייניות לחוק אוהם, נשקלו מנקודת המבט של שימוש בזרם ישר, בהתאם לזרם חילופין הכל נראה שונה במקצת.
בחינת השפעת החוק על כמות משתנה
המושג "התנגדות" לתנאים של העברת זרם חילופין צריך להיחשב יותר כמו המושג "עכבה". הכוונה היא לשילוב של עומס התנגדות (Ra) ועומס נגד תגובתי (Rr).
תופעות כאלה נגרמות על ידי הפרמטרים של אלמנטים אינדוקטיביים וחוקי המיתוג ביחס לערך מתח משתנה - ערך זרם סינוסואידי.
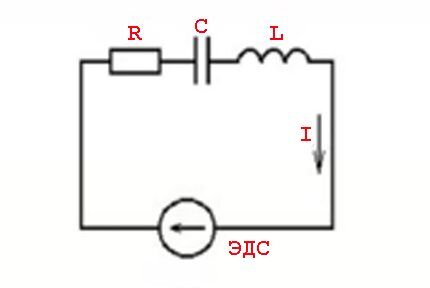
במילים אחרות, ישנה השפעה של ערכי זרם המובילים (פיגור) מערכי מתח, המלווה בהופעת כוחות אקטיביים (התנגדות) ותגובתיים (אינדוקטיביים או קיבוליים).
תופעות כאלה מחושבות באמצעות הנוסחה:
Z=U/I אוֹ Z = R + J * (Xל -איקסג)
איפה: ז - עכבה; ר - עומס פעיל; איקסל , איקסג - עומס אינדוקטיבי וקיבולי; י - מקדם.
חיבור טורי ומקביל של אלמנטים
עבור אלמנטים של מעגל חשמלי (קטע של מעגל), נקודה אופיינית היא חיבור טורי או מקביל.
בהתאם לכך, כל סוג של חיבור מלווה בדפוס שונה של זרימת זרם ואספקת מתח.בעניין זה, גם חוק אוהם מיושם בצורה שונה, בהתאם לאפשרות לכלול אלמנטים.
מעגל של אלמנטים התנגדות המחוברים בסדרה
ביחס לחיבור סדרתי (קטע של מעגל עם שני רכיבים), נעשה שימוש בניסוח הבא:
- אני = אני1 = אני2 ;
- U = U1 +U2 ;
- R = R1 + ר2
ניסוח זה מדגים בבירור כי ללא קשר למספר הרכיבים ההתנגדות המחוברים בסדרה, הזרם הזורם בקטע של המעגל אינו משתנה בערכו.
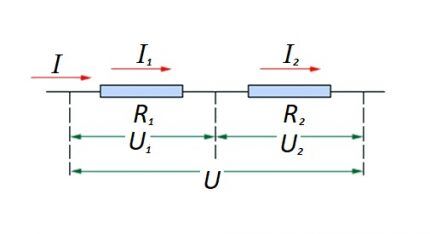
גודל המתח המופעל על רכיבי ההתנגדות האפקטיביים של המעגל הוא הסכום ומסכם את הערך של מקור ה-emf.
במקרה זה, המתח על כל רכיב בודד שווה ל: Ux = I * Rx.
ההתנגדות הכוללת צריכה להיחשב כסכום הערכים של כל הרכיבים ההתנגדות במעגל.
מעגל של אלמנטים התנגדות מחוברים במקביל
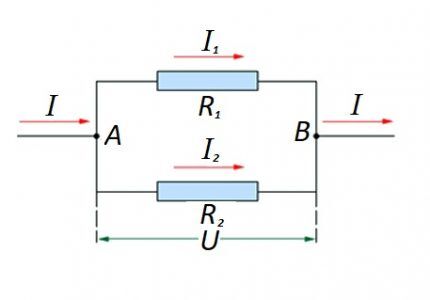
במקרה שבו יש חיבור מקביל של רכיבים התנגדות, הניסוח הבא נחשב הוגן ביחס לחוק הפיזיקאי הגרמני אוהם:
- אני = אני1 +אני2 … ;
- U = U1 =U2 … ;
- 1/R = 1/R1 + 1/R2 + …
אפשרויות ליצירת קטעי מעגל מסוג "מעורב", כאשר משתמשים בחיבורים מקבילים וטוריים, אינן נכללות.
עבור אפשרויות כאלה, החישוב מתבצע בדרך כלל על ידי חישוב תחילה של דירוג ההתנגדות של החיבור המקביל. ואז הערך של הנגד המחובר בסדרה מתווסף לתוצאה המתקבלת.
צורות אינטגרליות ודיפרנציאליות של החוק
כל הנקודות לעיל עם חישובים חלות על תנאים כאשר מוליכים של, כביכול, מבנה "הומוגני" משמשים במעגלים חשמליים.
בינתיים, בפועל, לעתים קרובות צריך להתמודד עם בניית סכמטיקה, שבה מבנה המוליכים משתנה בחתכים שונים. לדוגמה, משתמשים בחוטים בחתך גדול יותר או להיפך קטן יותר, עשויים מחומרים שונים.
כדי לקחת בחשבון הבדלים כאלה, יש וריאציה של מה שנקרא "חוק אוהם הדיפרנציאלי-אינטגרלי". עבור מוליך אינפיניטסימלי, רמת צפיפות הזרם מחושבת בהתאם לערך המתח והמוליכות.
הנוסחה הבאה משמשת לחישוב דיפרנציאלי: J = ό * E
לחישוב האינטגרלי, בהתאם, הניסוח הוא: I * R = φ1 – φ2 + έ
עם זאת, דוגמאות אלה קרובות יותר לבית הספר למתמטיקה גבוהה יותר ואינן משמשות בפועל בתרגול האמיתי של חשמלאי פשוט.
מסקנות וסרטון שימושי בנושא
ניתוח מפורט של חוק אוהם בסרטון למטה יעזור לבסס סוף סוף ידע בכיוון זה.
שיעור וידאו ייחודי מחזק באופן איכותי את המצגת הכתובה התיאורטית:
עבודתו של חשמלאי או פעילותו של מהנדס אלקטרוניקה קשורה באופן אינטגרלי לרגעים שבהם למעשה צריך לקיים את חוק גאורג אוהם בפעולה. אלו סוג של מציאות שכל איש מקצוע צריך לדעת.
ידע נרחב בנושא זה אינו נדרש - מספיק ללמוד את שלושת הווריאציות העיקריות של הניסוח על מנת ליישם אותו בהצלחה בפועל.
האם תרצה להשלים את החומר לעיל בהערות חשובות או להביע את דעתך? נא לכתוב הערות בבלוק מתחת למאמר. אם יש לך שאלות, אל תהסס לשאול את המומחים שלנו.



